- 1PS提示:因为图层已锁定,无法编辑图层的处理方法
- 2Adobe Illustrator CS5 序列号大全
- 3picacg苹果版怎么找不到|picacg ios版是不是下架了介绍
- 4ACDsee注册码免费分享(含ACDsee18、ACDsee10等版本)
- 5苹果iphone自动时间不准确的多种校正方法
- 6PDF浏览器能看3D文件吗?PDF浏览器看3D文件图文详细教程
- 7Potato(马铃薯聊天)怎么注册不了|Potato不能注册处理方法介绍
- 8Potato(土豆聊天)怎么换头像|Potato app更改头像方法介绍
- 9ipad版office如何激活? office365激活的图文说明教程
- 10最新的Adobe Illustrator CS4序列号大全
- 11Mac怎么通过设置VPN来登录youtube等国外网站
- 12qq邮件是否已读怎么看 QQ邮箱已经发出去的邮件怎么知道对方是否已经查看
在这篇文章中,我将使用C#编制两个寻找素数的算法,说明算法设计的重要性以及算法的分析。
素数寻找问题由来已久,一直是一些数学家追求的目的。关于素数的定义及性质,我就不在这里多叙了,相信大家都对此了如指掌。素数的寻找思路比较的简单,根据素数的性质(素数应该不能被除了1和它自身的其他数整除)我们可以从最小的素数2开始,一直到比它小1的数为止,用这些数去整除它,如果它能被整除则它必定不是素数,这是判断单个素数的方法(这个算法思想最简单,时间复杂度最大)。对于寻找比某一个给定的整数值小的所有素数也可以采用这种方法,不过我们会发现,采用这种单个判断的方法所耗的时间比较多。比如查找不大于10的素数,我们必须从2开始一个个判断,共需判断9个数,事实上按照我们后面讲述的方法,只需循环2次就可以了。因此,下面的两种方法都将基于删除法来做。
我们来看看删除法的思想:
1. 将小于给定整数值n的所有正整数加到一个数组中;
2. 删除能够被一些整数整除的数;
3. 数组中遗留的元素就是最后要得到的素数序列。
对于第二步,我们将给出两种方法来实现。我们先来看看算法:
算法一:
class prime
{
public static int[] PrimeList;
public static void FindPrime(int n)
{
int[] IntList;
IntList=new int[n];
for (int p=2;p<=n;p++) IntList[p-1]=p;
for (int p=2;p<Math.Sqrt(n);p++)
{
int j=p+1;
while (j<=n)
{
if ((IntList[j-1]!=0 ) && ((IntList[j-1]% p)==0) ) IntList[j-1]=0;
j=j+1;
}
}
int i=0;
for (int p=2;p<=n;p++)
{
if (IntList[p-1]!=0) i=i+1;
}
PrimeList=new int[i];
i=0;
for (int p=2;p<=n;p++)
{
if (IntList[p-1]!=0)
{
PrimeList[i]=IntList[p-1];
i=i+1;
}
}
}
}
这这个算法中,删除的数是那些被从2开始直到n的平方根的整数整除的数。这个算法比起前面介绍的单个素数的寻找方法要好,它的循环次数减少了一多半,但是这个算法还不是最理想的:
1. 例如,6既能被2整除,也能被3整除,那么当p=2时,6被删掉了一次;当p=3时,6又被删除了一次,虽然按照我们设定的算法规则,这不会导致冲突(通过判断IntList数组元素是否为0,若为0就不必重复删除),但是这会使得算法的效率低下。
2. 还有计算素数序列元素个数时,我们也走了弯路。第一步,我们先计算出了数组元素大小,第二步才开始赋值,事实上这两步我们可以减去计算数组大小这一步,可以把它放在前面完成。
3. 已经被删除了的元素,也就是那些不是素数的元素,可以不用拿他们去整除整数,例如4不用拿去整除8,因为能被4整除的数肯定能被2整除,已经在前面循环中被删除了。
基于上述考虑,我们得到了一个效率更加高的算法:
class primegood
{
public static int[] PrimeList;
public static void FindPrime(int n)
{
int[] IntList;
int len=n-1;
IntList=new int[n];
for (int p=2;p<=n;p++) IntList[p-1]=p;
for (int p=2;p<Math.Sqrt(n);p++)
{
if (IntList[p-1]==0) continue;
int j=p*p;
while (j<=n)
{
if (IntList[j-1]!=0 )
{
IntList[j-1]=0;
len=len-1;
}
j=j+p;
}
}
PrimeList=new int[len];
int i=0;
for (int p=2;p<=n;p++)
{
if (IntList[p-1]!=0)
{
PrimeList[i]=IntList[p-1];
i=i+1;
}
}
}
}
这个算法思想和前面的算法完全一样,不过改正了上面算法中不完善的一些内容。
为了说明这两个算法的效率区别,我们编制了如下的主程序来比较一下他们的差异:
static void Main()
{
Console.WriteLine("Start!");
DateTime mytime5=DateTime.Now;
primegood.FindPrime(100000);
/*for (int i=0;i<=primegood.PrimeList.Length-1;i++)
{
Console.WriteLine(primegood.PrimeList[i]);
}*/
DateTime mytime6=DateTime.Now;
TimeSpan timeadd3=mytime6-mytime5;
Console.WriteLine(timeadd3.Ticks);
DateTime mytime1=DateTime.Now;
prime.FindPrime(100000);
DateTime mytime2=DateTime.Now;
TimeSpan timeadd=mytime2-mytime1;
DateTime mytime3=DateTime.Now;
primegood.FindPrime(100000);
DateTime mytime4=DateTime.Now;
TimeSpan timeadd2=mytime4-mytime3;
Console.WriteLine(timeadd.Ticks);
Console.WriteLine(timeadd2.Ticks);
}
}
通过运行这个程序,可以发现他们的差别是如此的大(前面的算法所耗时间几乎是后面算法的30-60倍),参见下图:
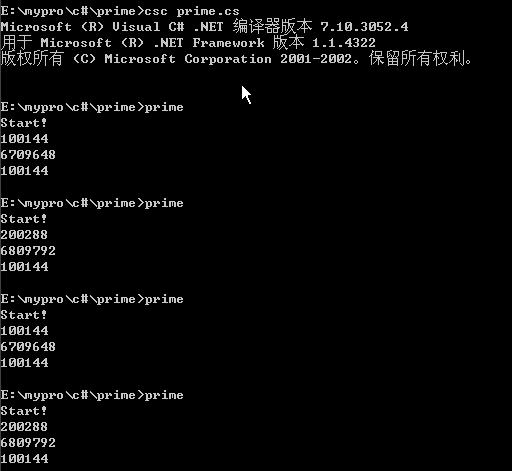
事实上,这两个算法的时间复杂度近似为:⊙(n1.5);⊙(n);可见,对于同一个问题有着多种不同复杂性的算法实现,算法设计是一门十分重要的学问。
推荐资讯 总人气榜

